courseraのMachineLearning(日本語字幕)をやってみる(3)その1(Week3前半)
Week3は、Logistic Regression(ロジスティック回帰)という、分類する方法(例:メールを、スパムと、スパムでないものに分類、)についての解説。
なるほど、さっぱりわからず、Quizも飛ばしまくりであったが、Programming Assignmentだけは、答えを見ながらやってみたい。
https://www.coursera.org/learn/machine-learning/programming/ixFof/logistic-regression
(環境)
Windows8.1
GNU Octave 4.0.3
(0)上記サイトから、machine-learning-ex2.zip をダウンロードして展開し、Octaveでex2フォルダを開く。
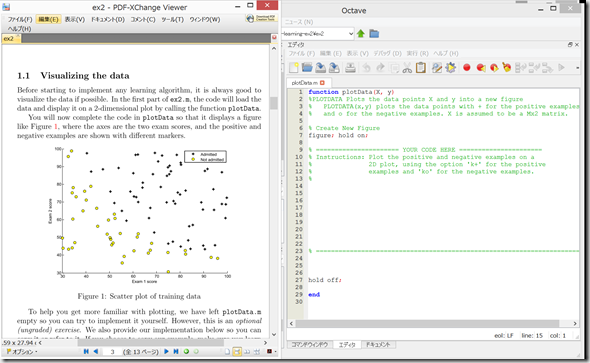
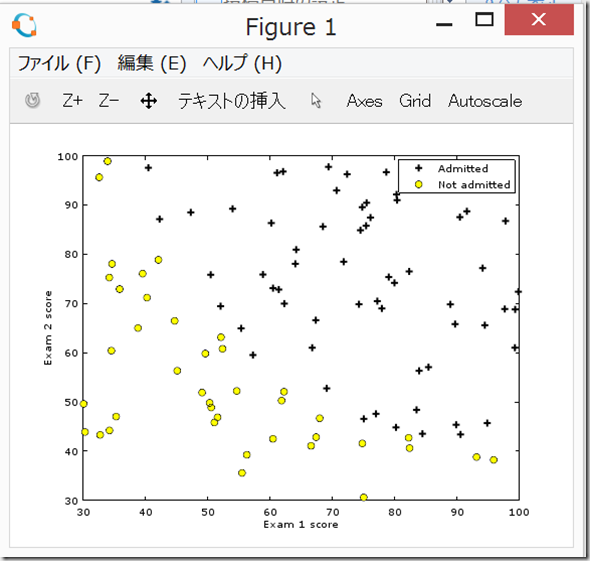
(1)1.1 Visualizing the data
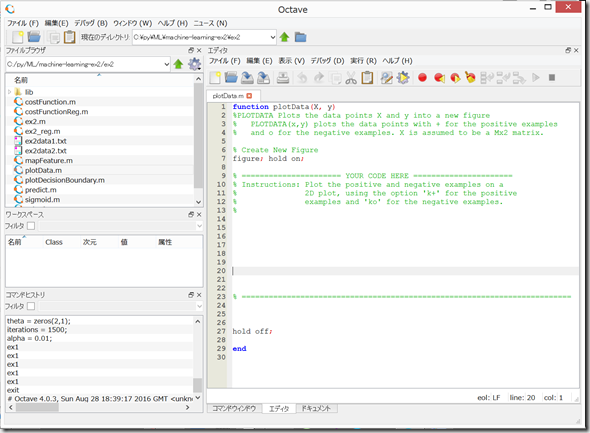
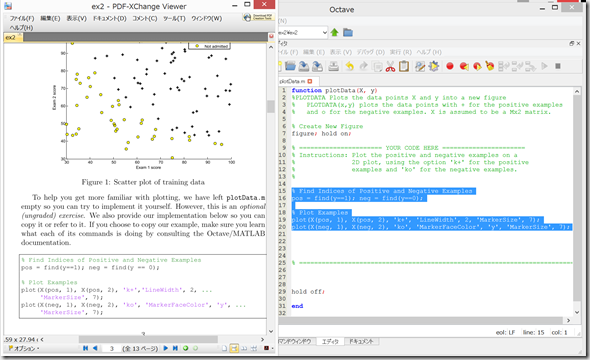
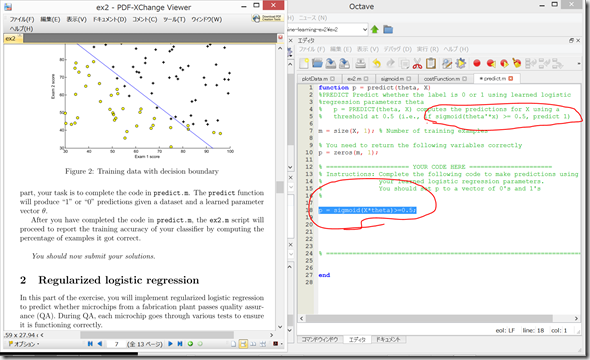
Octave上で、plotData.mを開き、PDFファイル記載の通りに記入して、保存。
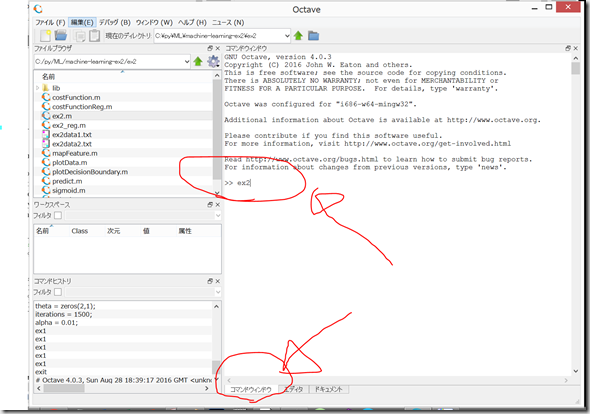
コマンドウィンドウで、 ex2 と記入して、「Enter」
ひとまずグラフのplotはできた。
何度も出てくる implement は、「実装する」という意味らしい。
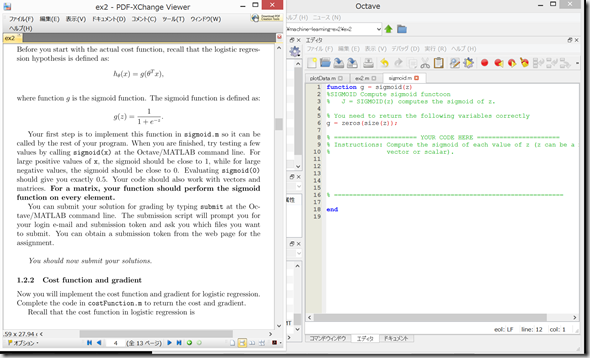
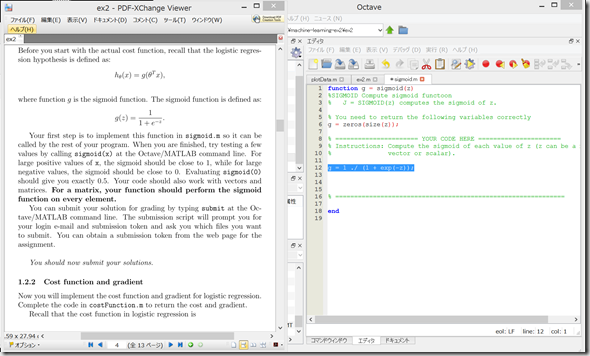
1.2.1 Warmup exercise: sigmoid function
sigmoid.m を開き、
sigmoid function シグモイド関数
を、octaveのコードを書けと言われても、、、本当に厳しい、、、そろそろ挫折の予感。。。
いつも通り答えをコピペ
https://github.com/kamu/ocw-assignments/blob/master/mlclass-ex2/sigmoid.m
cost function 目的関数
gradient 勾配、グラディエント、傾斜度
(参考)線形回帰と目的関数(cost function)について December 31, 2015
http://tech.mof-mof.co.jp/blog/machine-learning-cost-function.html
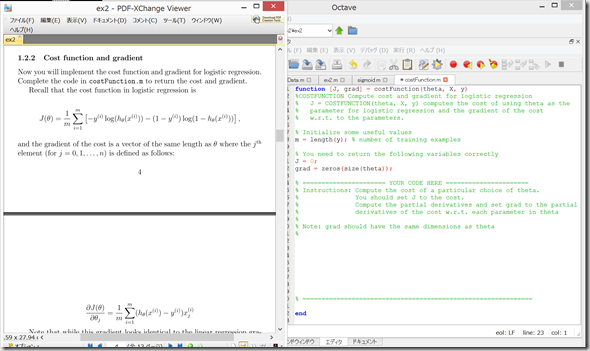
1.2.2 Cost function and gradient
cost function 目的関数
gradient 勾配、グラディエント、傾斜度
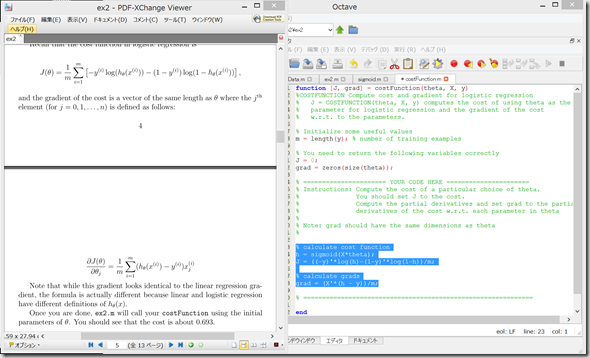
costFunction.m を開く。
% calculate cost function h = sigmoid(X*theta); J = ((-y)'*log(h)-(1-y)'*log(1-h))/m; % calculate grads grad = (X'*(h - y))/m;
(-y )’ の「’」のtranspose (転置行列)や、X’の「’」のtranspose(転置行列)がいまいちわかりにくい。
行ベクトルと、列ベクトルを入れ替えたりしているのだろうか?ううむ、いまいちわからん。
の式が、以下のようになっているらしい。。。
grad = (X’ * (h – y)) / m (式1)
octaveにおける、X’ は、Xの転置行列である。
ここでは、
ではなく、以下のような感じか。
(式1)の右辺は、次のようになるのだろう。こんな簡単なことでも、書き出さないと私にはわからない。。。パソコンで書くより、手書きでノートに記載した方が理解が早いであろう。
コマンドウィンドウで、「Enter」を押す。または、ex2 と入力して、「Enter」
1.2.3 Learning parameters using fminunc
f(Θ)を最小にするΘ(theta)を求めるために、fminunc という関数を使用するらしい。
fminuncを使用するためのコードは、既にex2.m に記載されているらしい。
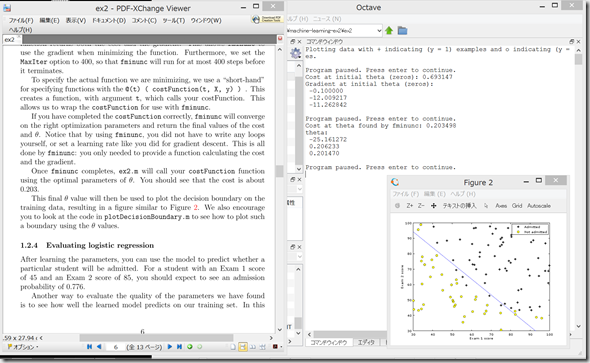
コマンドウィンドウで、「Enter」
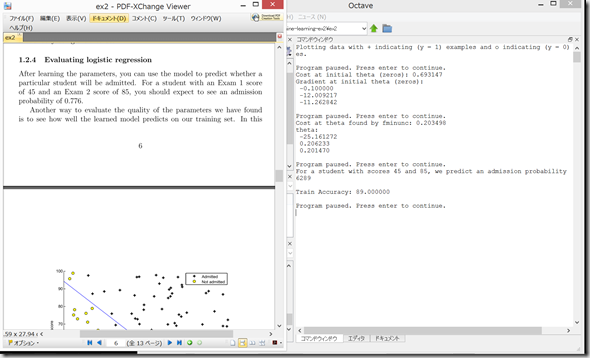
1.2.4 Evaluating logistic regression
学習したモデルを用いて、新たなXを入力して、入学試験に合格する確率を求める。
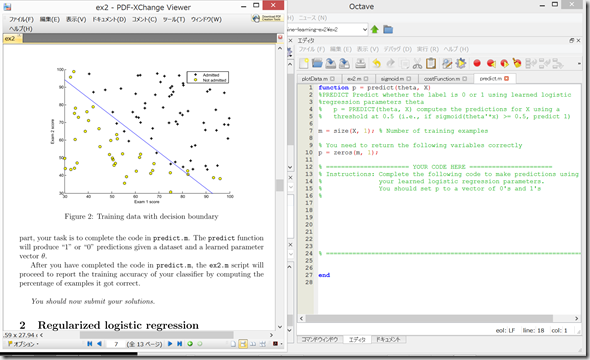
predict.m を開く。
(答えをコピペ)
p = sigmoid(X*theta)>=0.5;
なぜ0.5なのかさっぱりわからん。。。
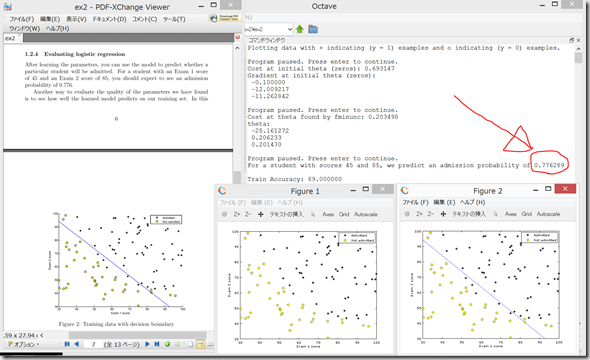
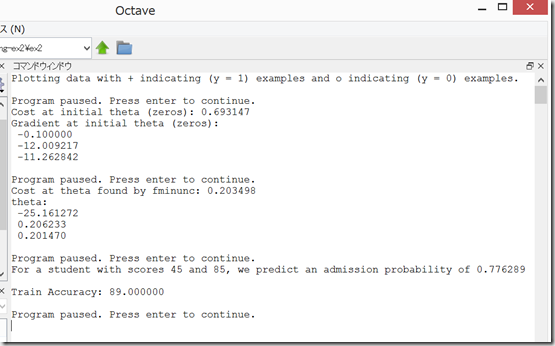
Exam 1で45点、Exam 2で85点の人がadmisssionとなる確率が0.776にならず、6289と表示されてしまった。どこで間違えたのか不明。
と思ったら、改行されていたのを見間違えていただけで、ちゃんと、0.776289になっていた。一安心。
ここまでで力尽きた、、、
(参考)
Coursera Machine Learningの課題をPythonで: ex2(ロジスティック回帰)
nokomitchが2015/10/20に投稿(2015/12/25に編集)
http://qiita.com/nokomitch/items/40fb63c40baa0239fb83
上記をコピペして、pythonでやってみる
(環境)
Windows8.1
Anaconda (python 3)
コマンドプロンプトを開いてex2フォルダに移動し、
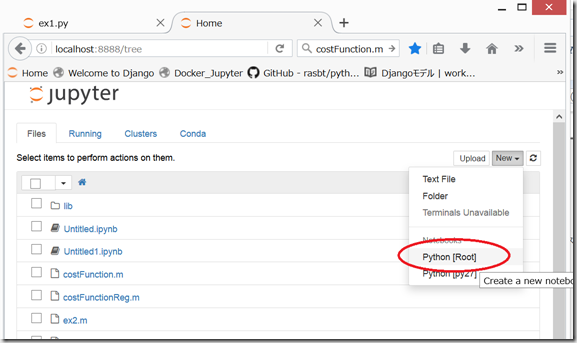
jupyter notebook
すると、ブラウザが立ち上がる。New .> Python[root]
http://qiita.com/nokomitch/items/40fb63c40baa0239fb83#python%E3%82%B3%E3%83%BC%E3%83%89
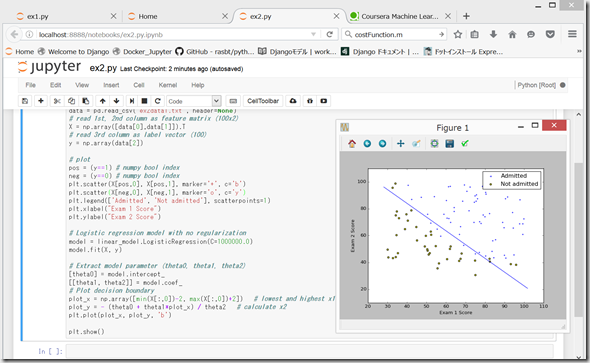
のコードをそのままコピペして、「Shift」+「Enter」
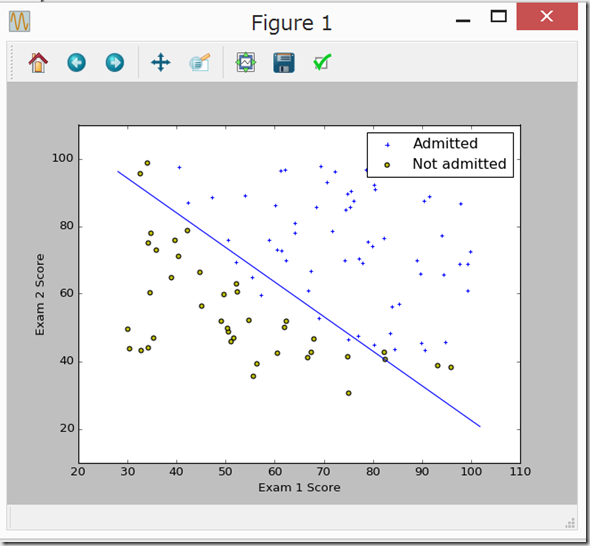
しばらく、busy… のあと、ちゃんと同じグラフが表示された。
「Exam 1で45点、Exam 2で85点の人がadmisssionとなる確率」はどのようにプログラムしたらよいのかな?気になるところだが、まあ、私には無理なのでまた後日、、、
(参考)
scikit-learnでロジスティック回帰[LogisticRegression][Titanic] 2016年4月27日
http://noumenon-th.net/programming/2016/04/27/logisticregression/
logistic regressionを使ってみる。classifyとprobabilityを出すあたりまで。
http://www.mwsoft.jp/programming/numpy/logistic_regression.html
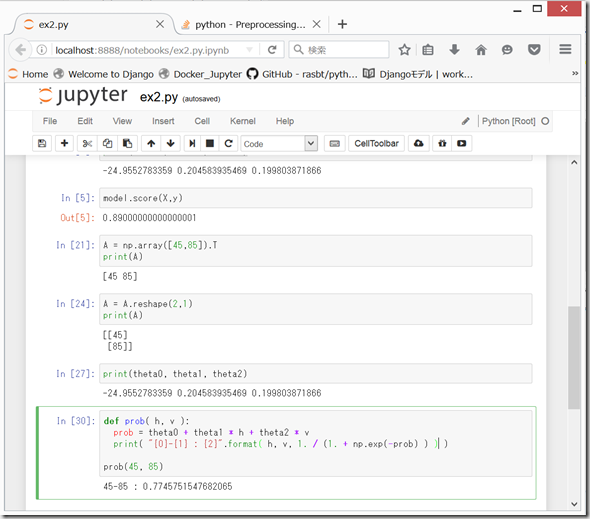
●「Exam 1で45点、Exam 2で85点の人がadmisssionとなる確率」
print(theta0, theta1, theta2)で、ベクトルΘを求めてから、
を求めればよいと思われる。
Exam 1で45点、Exam 2で85点の人は、x1=45, x2=85を上記に代入して、下記のように計算すると、
0.774575
という値が出てくるが、これは、微妙に、先ほどのOctaveで計算した「0.776289」と異なる。
しかし、Octaveで、fminuncで出したthetaの値は以下の通り。
Cost at theta found by fminunc: 0.203498
theta:
-25.161272
0.206233
0.201470
これらのΘを設定して再度計算すると、Pythonの方の計算でも、Octaveで計算したのと同じ、「0.776289」にかなり近くなって、一安心。
ふう。全くわからん。
しかし、これで、「2つのパラメータ(exam1とexam2の点数)に対して、0か1かの分類(入学試験の合格または不合格)」のデータがたくさん(100個くらい?)あったとき、pythonまたはOctaveで「ロジスティック回帰」で機械学習させて、新たな2つのパラメータから、「1(合格)」となる確率?を求めることができるようになった。(と思う。)
しかし、こんな面倒なことをしなくても、
EZR(Easy R)
http://www.jichi.ac.jp/saitama-sct/SaitamaHP.files/function.html
で、
①名義変数の解析 >
二値変数に対する多変量解析(ロジスティック回帰)
をすれば、一発でできるのであろう。。。まあ、勉強ということで、、、
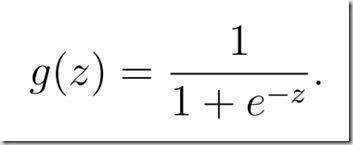
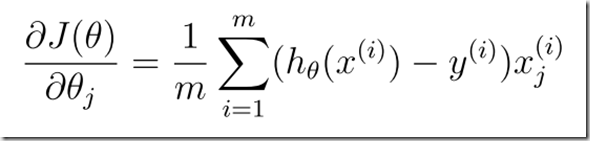
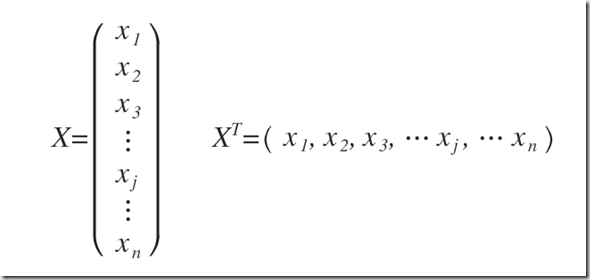
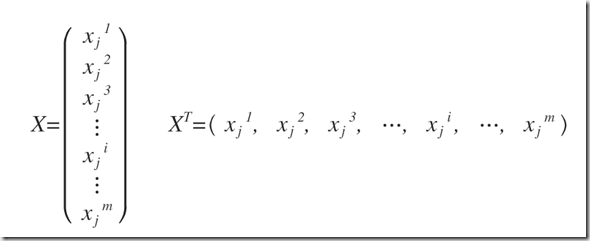
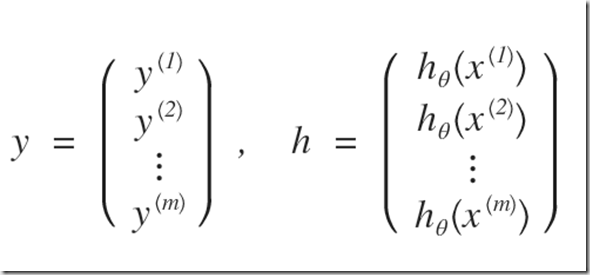
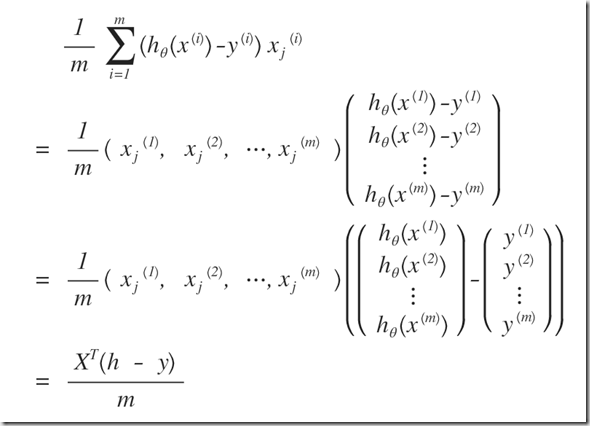
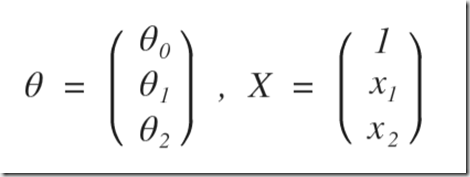
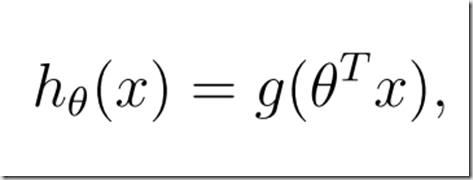
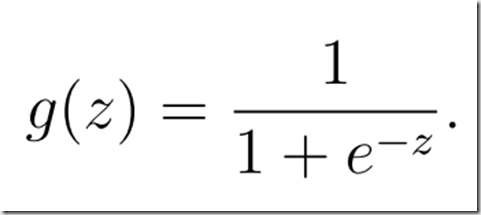


ディスカッション
コメント一覧
まだ、コメントがありません